|
L'ESPANSIONE ISLAMICA
Il 16 luglio dell'anno 622 d.C. il profeta Muhammad
(Maometto) fu costretto a fuggire dalla città della Mecca
verso Medina, dall'ostilità delle autorità politiche e
religiose che si vedevano minacciate dalla sua predicazione,
consistente essenzialmente nel rifiuto dei culti
politeistici e nell'esortazione alla venerazione di un unico
Dio. Nel giro di pochi anni Maometto rientrٍ in trionfo alla
Mecca (630), due anni prima della sua morte. Il
Calendario islamico (lunisolare) venne canonizzato nel
638 dal secondo califfo Omar. L'anno 1 del Calendario
islamico venne posto al 622 d.C.
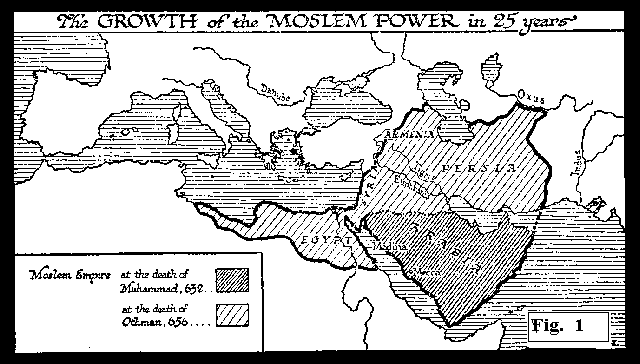
Dodici anni dopo la morte di Maometto, conclusa l'adesione
all'Islam (Islam = "sottomissione incondizionata") in
tutta la penisola arabica, incominciٍ l'espansione
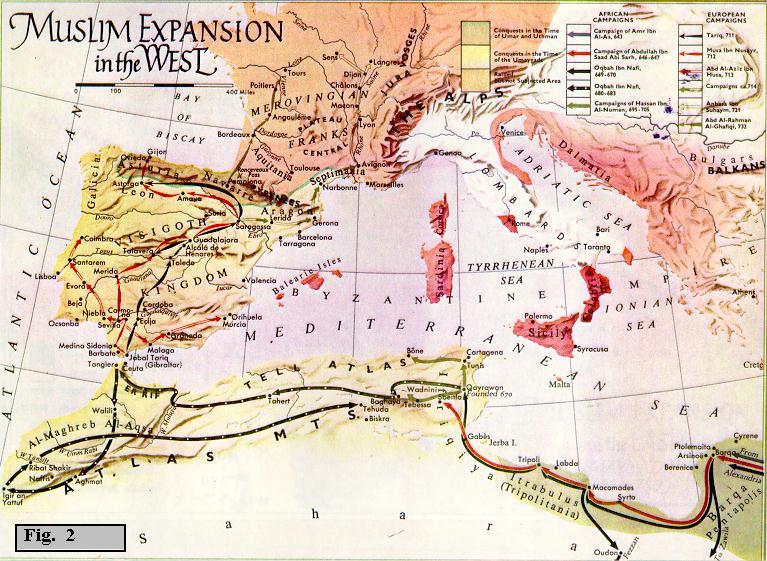
all'infuori di essa. Nel 709 l'intero Nordafrica era
conquistato. Dal 712 l'espansione si estese alla Spagna e si
arrestٍ soltanto nel 732 con la sconfitta di Poitiers
inflitta agli Islamici dai Franchi di Carlo Martello.
Verso est l'espansione si produsse con la conquista della
Persia e della Transoxiana.
La leadership dell'Islam è strettamente associata
all'affermazione di due dinastie, quella degli Omayyadi
e quella degli Abbassidi. Fondatore della prima
dinastia fu il califfo Muawiya I, il cui padre, un
tempo avversario di Maometto, era già riuscito a imporsi ai
suoi tempi. Stabilita la sede del califfato a Damasco,
questa dinastia raggiunse l'apice della sua potenza con il
califfo al-Walid (705 - 717) che, pur non riuscendo a
invadere l'Impero bizantino, estese il dominio dell'Islam
dai confini della Cina alla Spagna meridionale.
La religione e la cultura islamica si svilupparono nei due
filoni dottrinali principali sunnita e sciita.
Occorre dire che la religione islamica non venne imposta con
la forza ai popoli conquistati (per lo meno nella fase
successiva), non solo perchè era ritenuta esclusiva degli
Arabi, ma perchè il loro sistema fiscale era basato su tasse
che gravavano esclusivamente su sudditi non musulmani.
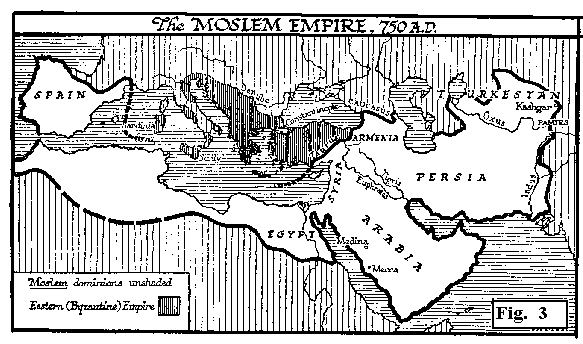
Una rivolta guidata dalla famiglia degli Abassidi
mise fine nel 750 al califfato omayyade. L'unico componente
della dinastia omayyade che riuscى a scampare al massacro fu
Abd ar-Rahman I che si rifugiٍ in Spagna dove occupٍ
Cordova e Siviglia, dando vita all'Emirato autonomo di
Andalusia.
Eponimo della dinastia Abasside fu al-Abbas,
zio di Maometto. Scacciati gli Omayyadi, gli Abbassidi
trasferirono la capitale da Damasco a Baghdad,
fondata nel 762 dal califfo al-Mansur (754 - 775).
I califfi abassidi riuscirono a mantenere sia il potere
politico che l'autorità religiosa per oltre un secolo. Il
massimo splendore della dinastia fu raggiunto con Harum
ar-Rashid. Alla sua morte, i due figli si contesero il
trono e prevalse al-Mamun. Da allora le lotte
intestine minarono il prestigio della famiglia che
attraversٍ una continua fase di debolezza che culminٍ alla
metà del XIII secolo quando i Mongoli si impossessarono di
Bagdad uccidendo l'ultimo califfo abasside.
Oggi nel filone dottrinale Sunnita è compresa la maggioranza
(circa l'83%) dei seguaci dell'Islam. Il nome deriva dal
concetto di Sunna, la tradizione più antica di norme
etiche e morali, stabilite sulla base dei detti e degli
scritti di Maometto, noti con il termine di Hadith, e
considerati, insieme con il Corano, le fonti principali del
diritto islamico. Nel secolo XIII furono accettate come
autentiche 14 collezioni di hadith.
L'altra corrente dell'Islam, quella degli Sciiti, si
distingue per le origini e le concezioni teologiche.
Originariamente il termine "sciiti" (da shiah =
seguace) stava ad indicare i sostenitori del partito di
Alى, genero di Maometto (avendone sposato la figlia
Fatima) e quarto califfo dell'Islam, che essi consideravano
unico successore legittimo del Profeta alla guida
dell'Islam, e quindi usurpatori i tre califfi precedenti.
Alى venne assassinato nel 661 (ancora oggi nella mistica
sciita questo fatto è considerato il martirio per
eccellenza, che consacra le loro rivendicazioni).
A questa prima fase di lotte a sfondo politico seguirono in
epoca omayyade (661 - 750) le tappe dell'elaborazione della
teologia caratteristica della comunità sciita. Custodi di
questa sapienza (trasmessa ad Alى direttamente da Maometto)
sarebbero i legittimi discendenti di Alى, che sono venerati
come iman, cioè "guide", della comunità, dotati di
poteri sovrannaturali, come l'infallibilità e la capacità di
compiere miracoli. Questa visione dottrinale si discosta
nettamente da quelle dei sunniti che riconoscono soltanto in
Maometto l'ultimo profeta, e che non ammettono poteri
soprannaturali degli iman.
Il mondo arabo non tardٍ a liberarsi del fanatismo che
inizialmente sostenne le conquiste militari (si ricordi
l'incendio della Biblioteca di Alessandria ordinato nel 641
dal califfo Omar in base al semplice sillogismo di ritenere
i libri in essa contenuti inutili se conformi alla fede
islamica e dannosi se contrari). Evidentemente quindi la
prima fase di espansione dell'Islam fu caratterizzata dalle
conquiste militari e dall'ardore della predicazione
religiosa. Ma, a partire dal nono secolo, venendo a contatto
con la cultura dei paesi conquistati, nel mondo islamico si
manifestٍ un vivissimo interesse per lo studio delle
discipline filosofiche, mediche e matematiche. In
particolare gli Arabi assimilarono la scienza e la filosofia
del Vicino Oriente ellenistico, attraverso le opere di
Aristotele, Platone, Euclide, Galeno, che venivano a mano a
mano tradotte in arabo.
Anche la conquista della Persia e dell'India si rivelٍ
grandemente benefica per la cultura araba, per i tesori
culturali che gli Arabi seppero trarre da quelle preziose
civilizzazioni.
Fra le scienze, particolarmente fecondo fu il travaso di
conoscenze astronomiche che gli Arabi acquisirono dai Greci.
Occorre tenere presente che gli astronomi arabi vennero a
contatto con l'astronomia greca attraverso due vie. Già fin
dai tempi della dinastia Achemenide (V secolo a.C.), che
aveva esteso la sua sovranità anche all'India di nord ovest,
alcune tecniche astronomiche babilonesi erano filtrate in
India. Durante il periodo Seleucide (IV e III secolo a.C.),
altre idee astronomiche, questa volta greche (pur miste ad
altre tecniche babilonesi) erano nuovamente filtrate in
India. Il risultato di queste trasmissioni culturali,
avidamente accolte dagli Indiani, fu che si ebbero testi
astronomici indiani (scoperti oggi) recanti le teorie degli
epicicli prima dell'epoca di Tolomeo. Poichè l'espansione
islamica dei secoli VI e VII si estese anche verso l'India,
questa acquisizione di idee astronomiche di origine greca fu
la prima via di contatto che gli Arabi ebbero con
l'astronomia ellenica. La seconda via fu quella più diretta
della traduzione delle opere greche, a partire dalla
conquista del Nordafrica, specificamente con la caduta di
Alessandria. |
|
RELIGIONE ISLAMICA E ASTRONOMIA
Alcuni collocano la nascita dell'astronomia araba all'epoca
in cui alcuni saggi indiani recatisi in visita presso la
corte di Al Mansour, califfo di Bagdad nel 744,
portarono con loro un trattato di astronomia pratica, che
subito fu tradotto in arabo con il titolo di “Tavole
astronomiche indiane” (“Zig al Sindhind”,
letteralmente canoni indiani) da Ibn Ibrahim al Fazari
e da Ya'qub Ibn al Tariq.
La religione islamica poneva all'astronomia un certo numero
di problemi. C'era anzitutto la necessità di disporre di un
efficiente calendario per osservare le ricorrenze religiose
alla data corretta. La seconda indicazione astronomica era
quella di fornire al credente una regola semplice ed
affidabile, la qibla, per consentirgli di
rivolgersi verso la Mecca al momento della preghiera.
Un'altra indicazione astronomica era quella di fornire al
muezzin il modo per chiamare i fedeli alla preghiera nelle
ore prescritte (su certi astrolabi arabi si avevano curve
per le ore delle preghiere). Ma non si deve pensare che a
motivare lo studio dell'astronomia presso gli Arabi siano
state unicamente queste ragioni di carattere pratico. Gli
Arabi dimostrarono di possedere un genuino amore per la
cultura, esaltandola come un dono prezioso proveniente da
Dio. Non poterono quindi non aderire pienamente all'ideale
ellenistico di amore per la cultura. |
|
L'INCONTRO CON L'ALMAGESTO
Il tipico manuale astronomico arabo era lo Zij.
Il prototipo più antico di Zij era una raccolta delle
Tabelle dell'Almagesto, accompagnate da un insieme di
regole. Uno Zij di successo fu quello redatto dal
famoso Al Khwarizmi, matematico ed astronomo vissuto
a Bagdad agli inizi del IX secolo. Oltre alle Tabelle,
incorporava anche materiale indiano e persiano. Venne
tradotto anche in latino.
Un altro Zij molto importante fu quello redatto da
Albatenio (al-Battani, 858 - 929), per gli elementi di
novità che conteneva, notevoli tra questi il nuovo valore di
obliquità dell'eclittica di 23؛ 35' e il nuovo valore della
longitudine dell'apogeo solare, entrambi trovati da al
Battani stesso. Questa seconda scoperta fu di enorme valore
perchè sanciva il fatto che l'apogeo solare era mobile
(l'astronomia alessandrina non era riuscita a pervenire a
questo risultato). Lo Zij di Albatenio incontrٍ un
favore maggiore del precedente perchè si rifaceva a metodi
più propriamente tolemaici. Anche l'opera principale di
Albatenio De scientia stellarum (nella dizione
latina) ebbe larga fama. Gli Zij che seguirono
questo, fino al secolo XV, furono compilati sulla falsariga
di questo di Al Battani.
La prima traduzione in arabo dell'Almagesto fu
eseguita, all'inizio del secolo IX è attribuita per
tradizione ad al Haggiag ibn Yussuf ibn Matar su
ordine originale del califfo Harum al Rashid, della
dinastia Abasside. Al Haggiag, della specola di Bagdad,
aveva tradotto anche i primi sei libri di Euclide. Il figlio
e successore di al-Rashid, il califfo al-Mamun (786 -
833), fece eseguire due traduzioni. Una di queste, eseguita
negli anni 827/827, da al-Haggiag, esiste tutt'ora.
L'altra traduzione araba esistente è quella eseguita intorno
all'892 da Ishaq ibn Hunayn, e in seguito revisionata
da Thabit ibn Qurra.
Al nome del grande ed illuminato sovrano al-Mamun sono
legate due eccezionali imprese astronomiche, eseguite da
suoi astronomi per suo espresso ordime: (1) la misurazione
estremamente precisa di 23؛ 33' dell'obliquità
dell'eclittica, nell'anno 830, e (2) l'altrettanto celebre
misura del grado di meridiano, nell'anno 828: due gruppi di
astronomi percorsero, in sensi inversi, un tratto di pianura
mesopotamica, misurando l'altezza del polo fino a trovare
una variazione di un grado, ottenendo il valore di
111.683,12 metri, valore pochissimo diverso dal reale, che
alla latitudine media della Mesopotamia è di 110.938,0
metri. E' possibile che a sovraintendere a entrambe le
misurazioni sia stato Alfragano (Ahmad ibn Muhammad
ibn Kathir al-Farghani), uno degli astronomi di al-Mamun,
autore del trattato Elementi di astronomia,
uno dei primi notissimi compendi dell'Almagesto,
tradotto in seguito da Gerardo da Cremona. |
|
CRITICHE A TOLOMEO
Un altro genere di trattati astronomici arabi furono i
commentari all'Almagesto. Col tempo, questi
commentari assunsero anche aspetti critici su alcuni punti
dell'opera che riuscivano poco covincenti.
La cosmologia tolemaica conobbe un diverso e contraddittorio
grado di interesse presso gli Arabi. Si ha la netta
impressione che il libro di Tolomeo Ipotesi planetarie
abbia avuto una scarsa circolazione nel mondo arabo (per lo
meno in confronto all'Almagesto). E' difficile
trovare opere arabe nelle quali vengano commentati
adeguatamente i due aspetti fondametali della cosmologia
tolemaica, e cioè il sistema delle sfere solide annidate e
le distanze planetarie. In genere, o è affrontato un
argomento o è affrontato l'altro. Nel trattato di cosmologia
tolemaica di Thabit, le distanze tra i pianeti sono
modificate rispetto a quelle di Tolomeo.
Thabit al Farghani nel suo Elementi di astronomia
sembra avere poca dimestichezza con l 'opera Ipotesi
planetarie di Tolomeo. E' a conoscenza della teoria
classica delle sfere annidate ma procede per suo conto nel
calcolo delle distanze.
Un aspetto qualificante dell'astronomia araba fu (malgrado
la linea fondamentalmente tolemaica) la presenza di numerose
critiche di certi aspetti dell'Almagesto. La prima
critica fu certamente quella di aver violato i canoni
aristotelici per aver adottato moti non uniformi, e per aver
introdotto l'equante. Una prima critica su questo soggetto
venne a Tolomeo da al Tusi (1201 - 1274).
Ibn al Haytham arrivٍ a scrivere un libro intitolato
Dubbi su Tolomeo. La critica di Haytham
raggiunse forse il vero punto focale perchè egli mise in
luce l'assurdità di descrivere dei moti di corpi celesti,
sulla base di semplici costruzioni geometriche che non
avevano alcun fondamento con la realtà, se non una apparenza
visuale. Mosé Maimonide (1135 - 1204,israelita) nella
sua Guida per i perplessi negٍ qualunque
valore alle costruzioni geometriche degli epicicli e degli
eccentri.
Questa visione critica di Tolomeo si consolidٍ in un gruppo
di astronomi che si associarono in un osservatorio a
Maragha, in Persia. Alla metà del XIII secolo, Ulugh
Beg, nipote di Gengis Khan, fondatore della dinastia
Ilkhani e conquistatore di Persia e Mesopotamia, si
lasciٍ persuadere dall'astronomo Nasir al Din al Tusi
a fondare e sostenere un notevole osservatorio a Maragha.
Nel 1272 gli astronomi operanti a Maragha completarono un
nuovo Zij, le Tavole Ilkhani.
Infine, una notevole modifica a Tolomeo fu prodotta da
Ibn al Shatir di Damasco, vissuto dal 1304 al 1375
circa, che eliminٍ l'equante, soltituendolo con un ulteriore
epiciclo. Malgrado queste innovazioni abbiano goduto di
larga fama nella comunità scientifica islamica, per le
modalità di computo delle posizioni planetarie si continuٍ a
rifarsi alla classica procedura tolemaica. Vedremo che
l'innovazione di al Shatir di eliminare l'equante, sarà
ripresa da Copernico, che potrebbe averla appresa, secondo
il parere di alcuni, durante i suoi prolungati soggiorni in
Italia. |
|
NOMI ARABI DELLE STELLE
Come è noto, molti nomi di stelle sono di derivazione araba.
Ne diamo alcuni esempi. Per l'Orsa Maggiore (Grande Carro),
abbiamo Dubhe derivato da Thar al Dubb al Akbar
("il dorso dell'orsa"), Merak da al Marakk
("il lombo dell'orsa"), Phedka da al Fahdah
("la coscia"), Alioth da Alyath ("grassa
coda"), Alkaid / Benetnash da al Ka'id
Banat al Na'ash ("governatore delle figlie della bara"),
Mizar da Mizar ("cavallo").
Nella costellazione dell'Orione ricordiamo Betelgeuse
da Na'beit al gueze ("spalla del gigante"), Rigel
da Rijil al jauzeh ("la gamba sinistra del gigante"). Del
Toro ricordiamo Aldebaran da Na'ir al dabaran
("colei che segue le Pleiadi"). Del Perseo Algol da
al Ghul ("spirito mutevole" con riferimento evidente
alla sua variabilità). Alcune altre stelle i cui nomi sono
di derivazione araba sono Achernar da Akher Nahr
("foce del fiume"), Altair da Al tair ("aquila
volante"), Vega da Al nasr al waki ("aquila
planante"). |
|
AL-KHWARIZMI
Abu Jafar Muhammad ibn Musa Al-Khwarizmi (ca. 780 -
850). Harum al-Rashid era califfo della dinastia
Abasside di Bagdad al tempo della nascita di al-Khwarizmi.
Dopo le conquiste militari (dal Mediterraneo all'India)
al-Rashid incominciٍ a favorire la fioritura culturale nel
suo regno. Alla morte di al-Rashid, il conflitto tra i due
figli si concluse con la soppressione del maggiore e il
trionfo del minore, al-Mamun, nell'813. Questi,
seguendo le orme del padre, continuٍ ad esercitare il suo
patronato su arti e scienze, fondando a Bagdad un'accademia
di sapienti, chiamata Casa della saggezza, dove ebbe
inizio il lavoro di traduzione di opere classiche greche.
Fondٍ anche una libreria dove vennero collezionati
manoscritti provenienti da Bisanzio e diversi osservatori
astronomici.
Al Khwarizmi iniziٍ la sua attività astronomica con
traduzioni dal greco, ma anche con la scrittura di suoi
lavori. Uno dei primi fu il trattato Hisab al-jabr wal
muqabala che è considerato la sua opera più importante e
il primo libro sull'algebra (la parola "al-Jabr", che si
riferisce ad un particolare passaggio nel procedimento
risolutivo delle equazioni detto “regola del trasporto”, è
la matrice della nostra parola Algebra). |
 |
|
Un altro lavoro matematico di al-Khwarizmi
di enorme importanza fu un trattato sulla numerazione
indo-araba. Nella traduzione latina, il titolo era
Algoritmi de numero Indorum (come dal primo lavoro
nacque la parola algebra, da questo, per derivazione
dal suo nome, nacque la parola algoritmo). Si tratta
chiaramente del sistema di numerazione posizionale decimale
usato dagli Indiani, con la probabile introduzione per la
prima volta della cifra zero.
Altro importante lavoro di al-Khwarizmi, questa volta in
astronomia fu Sindhind zij, un trattato astronomico,
basato su testi astronomici indiani che erano stati dati in
dono alla corte Abasside da una missione diplomatica
indiana, intorno all'anno 770, quindi uno dei primi contatti
degli arabi con l'astronomia indiana (calendari, calcolo
della posizione del Sole vero, della Luna e dei pianeti,
tavole di seni e tangenti, astronomia sferica, tavole
astrologiche). Al-Khwarizmi compilٍ due versioni di questa
sua opera, ma entrambe andarono perdute. Nel decimo secolo
un astronomo arabo, al-Majriti, eseguى una revisione
critica di una delle due versioni e questa venne tradotta da
Adelardo di Bath. Dell'altra versione del Sindhind
zij di al-Khwarizmi venne pure eseguita in seguito una
traduzione in latino. |
|
AL-FARGHANI (ALFRAGANUS)
Abul Abbas Ahmad ibn Muhammad ibn Kathir al-Farghani
(ca 800 - 870). Nacque a Farghana, nell'attuale Uzbekistan.
Fu uno dei più famosi astronomi al servizio del califfo
al-Mamun e dei suoi successori. Scrisse Kitab fi
al-Harakat al-Samawiya, "Elementi di astronomia", un
trattato elementare di astronomia tolemaica che ottenne
molta popolarità per la sua accessibilità. |
 |
|
Il trattato venne tradotto in latino nel
secolo XII e godette di popolarità anche in Europa fino al
tempo della Sphaera di Sacrobosco, con
successive traduzioni. La presenza di innumerevoli
manoscritti latini degli "Elementi" di al-Farghani
nelle biblioteche europee testimonia la grande popolarità
che ebbe la sua opera. Gli specialisti ritengono che fu
dagli "Elementi", nella traduzione di Gerardo da
Cremona, che Dante trasse le cognizioni astronomiche esposte
nel Convivio e nella Vita Nova. La sua
cosmologia rivela che egli ebbe una visione abbastanza
chiara del principio delle sfere annidate ma nessuna
dimestichezza con la cosmologia delle Ipotesi planetarie
di Tolomeo. A partire dai parametri dell'Almagesto
produsse un calcolo autonomo delle massime e minime distanze
di ogni sfera planetaria. Eseguى anche una determinazione
abbastanza precisa del diametro della Terra.
Il Fihrist ("Indice") scritto da Ibn al-Nadim
nel 987, attribuisce ad al-Farghani un'altra opera di
carattere astronomico: Kitab amal al-Rukhamat ("Libro
sulla costruzione di orologi solari"). Svolse anche attività
ingegneristica al servizio del suo sovrano, specialmente
nello scavo di canali. |
|
THABIT IBN QURRA
Al-Sabi Thabit ibn Qurra al-Harrani (ca. 826 - 901).
Nacque ad Harran, la località allora mesopotamica di Carre
(oggi turca) dove i Romani guidati da Crasso avevano subito
la famosa disfatta dai Parti. La sua famiglia apparteneva
alla setta religiosa dei Sabiani, nel culto della quale era
riconosciuta l'adorazione delle stelle. Il prenome Al-Sabi
mantenuto da Thabit, lascia supporre che egli non si sia
convertito all'Islam. La setta aveva mantenuto legami con la
cultura greca tanto che era rimasta la tradizione, per i
membri della setta, di praticare la lingua greca. Thabit,
oltre che naturalmente la lingua araba, aveva dimestichezza
sia con il greco che con il siriaco.
La famiglia facoltosa lo convinse ad andare a Bagdad per
ricevervi una adeguata istruzione matematica e medica. Al
suo ritorno ad Harran, a causa delle sue vedute filosofiche
troppo liberali acquisite durante gli studi a Bagdad,
dovette subire una persecuzione religiosa da parte degli
ambienti conservatori della sua setta e decise perciٍ di
emigrare definitivamente a Bagdad. Là si guadagnٍ la
protezione del califfo al-Mutadid, uno dei più
celebri della dinastia Abbasside, che lo nominٍ astronomo di
corte. |
 |
|
Ma una attività di enorme importanza alla
quale si dedicٍ Thabit fu quella della traduzione di opere
greche, specialmente di carattere matematico. Sappiamo che
le prime due traduzioni in arabo degli Elementi di
Euclide, andate perdute tranne che per alcuni frammenti,
furono eseguite da al Haggiag. Sono sopravvissuti
invece numerosi manoscritti, copie di una terza traduzione
degli Elementi eseguita da Hunayn ibn Ishak.
Thabit aveva sottoposto la traduzione di Hunayn a una
revisione critica. Gli specialisti hanno accertato che la
gran parte delle successive versioni arabe degli Elementi,
si basarono su questa revisione di Thabit.
Ma Thabit non fu soltanto un provetto traduttore di opere
greche. Fu un brillante matematico che diede notevoli
contributi allo sviluppo di questa scienza.
Thabit scrisse anche opere astronomiche nelle quali si fa un
grande uso di matematica. La sua opera più conosciuta è
Del moto dell'ottava sfera (andata perduta), nella quale
venne sviluppata la teoria della trepidazione (movimento
oscillatorio degli equinozi e di tutta l'eclittica, al quale
dedicheremo un paragrafo in seguito).
Altri suoi lavori astronomici sono giunti fino a noi e sono
considerati fondamentali per aver consolidato
matematicamente la giovane scienza astronomica araba del suo
tempo. In particolare si occupٍ in maniera attenta e
meticolosa dei moti della Luna e del Sole, ritenendo che
l'osservazione delle eclissi di Sole e di Luna fossero
l'unico modo per determinare la posizione della Luna con
esattezza e che dalla durata del ciclo delle eclissi fosse
possibile determinare la periodicità dei moti del Sole e
della Luna con una semplice divisione (in ciٍ riprese
analoghi studi di Tolomeo). |
|
AL-BATTANI (ALBATENIUS)
Abu Abdallah Mohammad ibn Jabir Al-Battani (ca. 850 -
929). Anche lui, come Thabit Qurra, nacque ad Harran e anche
la sua famiglia apparteneva alla setta dei Sabiani. Ma si
ritiene che il nome "Abu Allah Muhammad" indichi che
Al-Battani, a differenza di Thabit Qurra, fosse di fede
islamica. Dunque, di una generazione più giovane di Thabit,
non si puٍ escludere che i due si siano frequentati.
Incominciٍ la sua carriera di osservatore astronomico (e di
fabbricante di strumenti astronomici) nelle località siriane
di Ar-Raqqah e di Antiochia. Esiste una documentazione (Fihrist,
"Indice"), del secolo X attestante il livello elevato della
fama di cui era gratificato al suo tempo sia per la qualità
delle sue osservazioni astronomiche che per le sue opere.
Secondo questo Fihrist egli osservٍ tra gli anni 877
e 918, mentre il suo catalogo stellare è dell'anno 880. I
suoi lavori elencati nel Fihrist sono Kitab al-Zij
e un commentario al Tetrabiblos di Tolomeo. |
 |
|
Il Kitab al-Zij è la sua più
importante opera. Comprende 57 capitoli nei quali gli
argomenti si succedono secondo lo schema classico degli Zij:
introduzione di strumenti matematici, teoria astronomica,
tavole.
Vediamo in breve quali furono i più importanti risultati
conseguiti da Al-Battani. Diede un catalogo di 489 stelle.
Perfezionٍ l'accertamento della durata dell'anno a 365
giorni, 5 ore, 48 minuti, 24 secondi. Diede per la
precessione degli equinozi il valore annuale di 54".5 e di
23؛ 35' per l'obliquità dell'eclittica. Accertٍ la
progressione della longitudine dell'apogeo solare e la
possibilità di avere anche eclissi di Sole anulari. Secondo
alcuni, perٍ, l'autorità di Tolomeo al tempo di Al-Battani
era tanto grande che, malgrado i suoi calcoli gli avessero
fatto determinare che la distanza del Sole si scostava
notevolmente da quella stabilita da Tolomeo, non osٍ
affermarlo pubblicamente. Dove invece manifestٍ con
chiarezza la propria contestazione a Tolomeo fu nel metodo
tolemaico di determinazione del diametro apparente della
Luna: al-Battani afferma infatti che la Luna puٍ assumere un
diametro apparente minore di quello del Sole e ciٍ spiega
perché si verificano le eclissi anulari. Afferma poi che lo
stesso diametro solare puٍ variare, contrariamente a quanto
sosteneva Tolomeo.
I commentatori sono concordi nell'affermare che l'importanza
di Al-Battani nello sviluppo della scienza si manifestٍ
specialmente nell'influenza che le sue opere ebbero su
scienziati quali Copernico, Brahe e Galileo.
Il Kitab al-Zij di Al-Battani venne tradotto in
latino nel 1116 da Platone da Tivoli con il titolo
De motu stellarum. Un'altra traduzione venne eseguita
nel XIII secolo in Spagna, ed entrambe fortunatamente ci
sono pervenute. |
|
IBN YUNUS
Abul Hasan Ali Abd al-Rahman ibn Yunus (ca. 950 -
1009).
Nacque in Egitto, probabilmente al Cairo, da una famiglia
che aveva dato illustri studiosi. In Egitto regnava la
dinastia Fatimide che aveva tratto il nome per
discendenza da Fatima, la figlia di Maometto.
Questa dinastia era riuscita a imporsi sulla Abbasside,
conquistando nella prima metà del secolo X il Nordafrica e
la Sicilia.
Ibn Yunus divenne un protetto del califfo Al-Aziz
che, malgrado fosse sempre impegnato in operazioni militari
fino all'ultimo giorno della sua vita, lo favorى nel
consentirgli di iniziare la sua attività astronomica. Dopo
la morte di Al-Aziz il califfato passٍ al figlio al-Hakim
e si ritiene che anche lui abbia continuato a proteggere
l'attività astronomica di Ibn Yunus, sebbene sembra che il
nuovo sovrano fosse più interessato ai responsi astrologici
del suo protetto.
Il suo lavoro più importante fu uno Zij: al-Zij al-Hakimi
al-kabir, dedicato, come dice il titolo, al sovrano. Di
81 capitoli, conteneva osservazioni eseguite da Yunus e da
suoi predecessori, una caratteristica questa piuttosto
singolare (gli altri autori, in genere, non facevano
distinzione tra le proprie osservazioni e quelle di altri).
La gran parte del materiale di quest'opera di Yunus era
costituita da tavole di vario tipo alle quali fecero ricorso
anche altri autori di epoche successive.
I suoi biografi sono concordi nell'affermare che predisse la
data della sua morte con sette giorni di anticipo, che si
ritirٍ in casa ad attenderla serenamente recitando versetti
del Corano. |
|
AL-HAITHAN (ALHAZEN)
Abu Ali Hasan Ibn al-Haithan (Alhazen) (ca. 965 -
1040). Nacque a Bassora, nell'attuale Irak meridionale.
Ricevette la sua educazione a Bagdad. E' considerato il
padre dell'ottica moderna. Trascorse la maggior parte della
sua vita in Spagna, dove condusse ricerche di ottica,
matematica e fisica.
Studiٍ la rifrazione della luce attraverso l'aria e l'acqua,
giungendo a scoprire le leggi della rifrazione. Arrivٍ molto
vicino a scoprire le leggi delle lenti di ingrandimento.
Il suo libro Kitab-al-Manazir tradotto in latino con
"Opticae thesaurus" servى da base per le ricerche
sull'ottica di Roger Bacon, Pole Witelo, Leonardo da Vinci e
Keplero.
Contraddisse la credenza che risaliva a Euclide e Tolomeo,
secondo i quali la visione era dovuta a raggi emessi
dall'occhio, affermando invece che i raggi visivi
provenivano dagli oggetti. Contraddisse anche la
introduzione dell'equante da parte di Tolomeo, perٍ
unicamente sulla base della violazione dei principi della
fisica aristotelica. A lui sono attribuiti i primi
esperimenti sull'uso della camera oscura. Scrisse più di
duecento libri dei quali solo pochissimi sono sopravvissuti.
|
 |
|
AL-BIRUNI
Abu Arrayhan Muhammad ibn Ahmad al-Biruni (973 -
1048). Nacque nell'attuale Karakalpakstan (Uzbekistan) a
Kwarizm, sul Lago d'Aral. Il suo luogo natale oggi è
chiamato Biruni, in suo onore. Iniziٍ i suoi studi sotto la
guida del famoso astronomo e matematico Abu Nasr Mansur.
Nel 990, giovanissimo eseguى la misurazione della latitudine
del suo luogo natale. All'età di 22 anni aveva già portato a
termine una serie di brevi scritti scientifici, uno dei
quali Cartografia, un trattato sulle proiezioni che è
sopravvissuto e che, oltre a sue idee originali, mostra una
vasta cultura sull'argomento per le estese citazioni su
altre opere. |
 |
|
Nel 995 la famiglia regnante, Banu Iraq,
venne rovesciata da un colpo di stato ed al-Biruni dovette
mettersi in salvo. Non è chiaro sapere cosa accadde in
questo frangente al suo maestro Abu Nasr Mansur, che era un
principe di quella famiglia. Si sa che nella città di Ravy,
presso l'attuale Teheran, riuscى a svolgere attività
astronomica negli anni dal 995 al 997, ma sempre sotto
l'assillo di ristrettezze economiche. In questo periodo ebbe
modo anche di collaborare con il famoso Abul Wafa.
Essi decisero di osservare una eclisse di Luna, (24 maggio
997), al Biruni a Kath, e Abul Wafa a Bagdad, in modo da
ricavare la differenza di longitudine tra le due località.
Si sa che intorno all'anno 1000 dedicٍ il suo libro
Cronologia a Qabus, regnante sullo stato di Ziyarid, dal
che dobbiamo arguire che gli aveva accordato la sua
protezione. In questo libro al-Biruni cita anche sette sue
opere precedenti, una delle quali soltanto di argomento
storico e le rimanenti tutte di argomento astronomico.
Sappiamo che il 4 giugno 1004 egli era di ritorno al suo
luogo natale perchè quel giorno osservٍ un eclisse di Luna.
Nel 1004, regnando su quel territorio Abul Abbas Mamun,
al-Biruni potè fruire del suo generoso supporto, che, forse
per intercessione di al-Biruni stesso, il signore estese
anche al vecchiuo maestro di al-Biruni, il principe Abu Nasr
Mansur, per cui i due scienziati ebbero la ventura di
tornare a lavorare assieme. Ma la guerra doveva nuovamente
interrompere gli studi di al-Biruni. Nel 1017 la regione
venne occupata militarmente e passٍ sotto il controllo del
sovrano di Ghazna al-Mahmud e i due scienziati, virtualmente
prigionieri del nuovo sovrano, dovettero seguirlo a Ghazna.
Il periodo che segue è piuttosto di difficile
interpretazione perchè sembra che, malgrado al-Biruni abbia
potuto svolgere una certa attività scientifica, abbia dovuto
subire al contempo anche delle privazioni.
La complessità della relazione tra al-Biruni e il suo
signore Mahmud è deducibile anche dal fatto che al-Biruni
dovette seguirlo durante una campagna militare che il
sovrano condusse in India, durante la quale al-Biruni ebbe
modo di eseguire determinazioni di latitudini di diverse
località del Punjab fino ai confini del Kashmir. Di questa
esperienza indiana al-Biruni lasciٍ una descrizione in una
sua opera famosa, India, che ci è pervenuta. Si
tratta di un'opera di enorme importanza per la gran quantità
di notizie su diversi aspetti di quel paese: la religione,
le tendenze filosofiche, il sistema di caste e le usanze
matrimoniali. Al-Biruni studia poi il sistema di scrittura e
quello di numerazione. Infine viene studiata l'astronomia ,
l'astrologia e il calendario indiani.
Al-Biruni studiava la letteratura indiana dall'originale
sanscrito del quale era un esperto traduttore in arabo.
Affrontava in questa lingua gli argomenti più disparati,
quali astronomia, astrologia, cronologia, geografia,
grammatica, matematica, medicina, filosofia, religione,
sistemi di pesi e misure.
Il sovrano Mahmud morى nel 1030 e il potere passٍ al figlio
anziano Masud, che sembra aver trattato Al-Biruni meglio di
quanto aveva fatto il padre, perchè godette di una
sostanziale libertà di movimento.
Masud venne assassinato nel 1040 e a lui successe il figlio
Mawdud. La produzione di scritti da parte di Al-Biruni fu
impressionante. E' stato calcolato che egli abbia prodotto
non meno di 146 trattati, per un totale di circa 13.000
pagine.
E' stato messo in evidenza dai commentatori l'approccio
rigorosamente scientifico che Al-Biruni ebbe nel trattare i
suoi argomenti. Per esempio nella trattazione dei dati,
contrariamente a Tolomeo che aveva l'abitudine di
selezionare i dati spesso quando si accordavano con le sue
teorie. Al-Biruni invece, quando decideva di scegliere un
dato, citava anche quelli che non si accordavano con quello
scelto. Poneva una particolare cura negli arrotondamenti e
anche nell'osservare grandezze che richiedevano il minimo di
manipolazioni.
Uno dei più importanti testi di Al-Biruni ha per titolo
Ombre, che si ritiene sia stato scritto intorno al 1021.
Costituisce una importante sorgente per la conoscenza della
storia della matematica e della fisica. Contiene una gran
quantità di nozioni su fenomeni riguardanti l'utilizzazione
delle ombre per la soluzione di problemi scientifici.
Contiene anche importanti idee sui moti accelerati e quelli
uniformi, sull'uso di un sistema di riferimento a tre
coordinate.
A lui viene attribuito il primo uso delle funzioni
trigonometriche (il seno si ritiene derivi dalla
latinizzazione “sinus” di una parola araba che significa
semicorda). Una argomentazione in cui manifestٍ una certa
indipendenza da Tolomeo fu nel ritenere possibile, in linea
teorica, la rotazione della Terra (Tolomeo affermava che se
la Terra ruotasse i corpi non cadrebbero verticalmente ma
verrebbero trascinati dalla rotazione. Per al-Biruni,
invece, ogni corpo è trascinato dalla rotazione della Terra
lungo la verticale di caduta.
Un aspetto importante dell'attività scientifica di Al-Biruni
è dato dalla corrispondenza che intrattenne con altri
scienziati. Ebbe un lungo e costante rapporto di
collaborazione con il suo maestro Abu Nasr Mansur: ciascuno
dei due chiedeva all'altro di affrontare specifici aspetti
di un proprio lavoro. Corrispose con il grande Avicenna
contrapponendosi a lui su argomenti quali la natura della
luce e del calore, ma anche su argomenti astronomici e
filosofici. Ebbe corrispondenza anche con al-Sijzi.
Circa la personalità di questo grande scienziato, vale la
pena di ricordare che in lui splendette uno dei tratti che
suscitano la nostra ammirazione per l'attitudine di
tolleranza di cui gli Arabi seppero dar prova in tante
circostanze. Al-Biruni non mancٍ di esprimere il suo dolore
nell'apprendere che conquistatori arabi di Khwarazm avevano
distrutto testi antichi di altra religione. |
|
IBN SINA (AVICENNA)
Abu Ali al-Husain ibn Abdallah ibn Sina (980 - 1037).
Nacque presso Bukhara, nell'attuale Uzbekistan e morى ad
Hamadan in Persia. E' largamente conosciuto con
l'appellativo occidentale Avicenna, anche se oggi si
tende a tornare alla versione originale del nome, Ibn Sina.
Si conosce molto della sua vita perchè egli stesso scrisse
un'autobiografia ed uno dei suoi studenti scrisse una sua
biografia.
Dopo la conquista araba della Persia, la prima dinastia
araba a imporsi fu quella Samanide, a partire dal 900.
Quando Avicenna nacque il sultano samanide era Nuh ibn
Mansur e il suo potere era in declino. Il padre di Avicenna
era governatore di un villaggio. La sua casa era un luogo di
ritrovo per persone colte che manifestarono presto il loro
stupore per la precocità del giovane Ibn Sina.
All'età di tredici anni incominciٍ a studiare medicina e a
sedici anni incominciava a trattare pazienti. La sua fama
medica crebbe al punto che il sovrano samanide Nuh ibn
Mansur acconsentى a sottoporsi alle sue cure e, per
ricompensa del trattamento positivo ricevuto, gli permise di
consultare la biblioteca reale.
Purtroppo gli anni che seguirono non furono favorevoli per
Ibn Sina, a causa delle lotte che si svilupparono per la
supremazia in Asia centrale. |
 |
|
Avicenna scrisse circa 450 opere, delle
quali circa 240 sono sopravvissute. Di queste 150 trattano
di argomenti filosofici mentre 40 sono dedicate alla
medicina. Questi sono i due campi nei quali si esercitٍ
maggiormente il suo sapere. Ma egli scrisse anche di
psicologia, geologia, matematica, astronomia e logica. Il
suo più importante lavoro matematico fu un'immensa opera
enciclopedica il Kitab al-Shifa, "Il libro delle
cure". Una delle quattro parti del libro è dedicata alla
matematica, in cui è trattata anche l'astronomia. Ibn Sina
suddivideva l'astronomia in tavole astronomiche, tavole
geografiche e calendario.
Eseguى anche osservazioni astronomiche, e sappiamo che
alcune vennero eseguite a Isfahan e altre ad Hamadan.
Inventٍ anche uno strumento astronomico mediante il quale
era possibile osservare sia l'altezza di un astro che il suo
azimut. |
|
AL-ZARQALI (ARZACHEL)
Abu Ishaq Ibrahim ibn Yahya al-Zarqali (1028 - 1087).
Conosciuto in Occidente con il nome di Arzachel,
svolse la sua attività di astronomo a Toledo, principalmente
con la compilazione delle famose Tavole toledane che
acquisirono grande fama in Occidente dopo la loro traduzione
in latino. Apportٍ molte correzioni a dati geografici che
risalivano a Tolomeo e al al-Khwarizmi. Diede per il valore
annuo del moto dell'apogeo solare il valore
straordinariamente preciso di 12" di arco. A lui è
attribuita l'invenzione di un particolare astrolabio che
venne chiamato Safilah e che venne descritto in molte
lingue.
Copernico esprime nel De revolutionibus la sua
riconoscenza ad al-Battani e ad al-Zarqali. |
|
AL-BITRUJI (ALPETRAGIUS)
Nur al-Din Ibn Ishaq al-Bitruji (ca. 1120 - 1204).
Originario del Marocco, emigrٍ in Spagna e visse
principalmente a Siviglia. La sua opera principale fu
Kitab al-Hayah che venne tradotta dapprima in ebraico e
poi in latino. Tentٍ di apportare modifiche al sistema
tolemaico, ma ne fu impedito dal volersi mantenere fedele ai
canoni aristotelici di perfezione dei moti circolari. |
|
AL-TUSI
Nasir al-Din al-Tusi (1201 - 1274) nacqua a Tus,
nell'attuale Iran. Fu uno dei più grandi scienziati del suo
tempo. Scrisse trattati di Algebra, aritmetica,
trigonometria, fisica, geometria, logica, medicina,
teologia. Venne protetto dal sovrano mongolo Hulug Begh
che, impressionato dalla sua cultura (e probabilmente dalla
sua abilità astrologica) lo nominٍ tra i suoi ministri.
Nel 1262 la munificienza del sovrano gli permise di
costruire un osservatorio astronomico a Maragha e
iniziٍ a sovraintendere all'attività di osservazione.
L'osservatorio era dotato della migliore strumentazione, tra
cui un quadrante murale di quaranta metri di raggio. Al-Tusi
stesso progettٍ altri strumenti di sua concezione. Produsse
delle tavole planetarie di straordinaria precisione ed un
catalogo stellare, pubblicando il tutto con il titolo
Al-Zij Ilkhani. Calcolٍ il valore di 51" quale rateo
annuo della precessione degli equinozi. Fu forse il primo
matematico a tentare di dimostrare il V postulato di
Euclide, e fu anche tra i primi a mettere in evidenza
notevoli improprietà nella dottrina tolemaica. In
particolare si mostrٍ scettico sull'equante come punto
rispetto al quale un moto non uniforme su un cerchio, poteva
essere visto uniforme. In un'altra sua pubblicazione,
Tadhkira Fi Ilm Al-Haya, "Memoria sull'astronomia",
diede una versione critica della teoria tolemaica. Nello
stesso libro propose un ingegnoso dispositivo che poteva
essere usato nelle teorie planetarie: si trattava della
dimostrazione che un moto oscillatorio rettilineo poteva
essere prodotto dalla combinazione di due moti circolari
(questo dispositivo oggi è spesso chiamato "la coppia di
Al-Tusi"). Ciٍ era chiaramente in contrasto con la rigida
distinzione operata da Aristotele tra i moti circolari
uniformi (che erano riservati all'ambito delle sfere
celesti) e i moti rettilinei (che erano propri del mondo
sublunare). |
 |
|
I suoi studi di trigonometria sferica
inclusero sei formule per la soluzione di triangoli
rettangoli sferici. Fu il primo a trattare la trigonometria
piana e sferica come una branca speciale della matematica.
Al-Tusi fu un prolifico scrittore. Sessantaquattro suoi
trattati sono sopravvissuti e furono tutti tradotti in
latino e nelle principali lingue europee. |
|
LA TREPIDAZIONE
Diamo ora una descrizione sommaria della teoria della
trepidazione perchè essa è attribuita, nella sua forma
originale, a Thabit Qurra. Abbiamo visto che non appena
l'astronomia araba, pur mantenendosi sostanzialmente nel
solco della tradizione tolemaica, si avviٍ verso una sua
autonoma operatività, non tardarono ad essere eseguite
scoperte sensazionali, propiziate evidentemente da
miglioramenti tecnologici strumentali di sette secoli, ma
anche dalla autentica passione con cui gli Arabi si
dedicarono a questa scienza. Abbiamo visto che Albatenio
(che è considerato il più grande astronomo arabo) trovٍ per
l'obliquità dell'eclittica il valore di 23؛ 33', ben più
piccolo del valore ricevuto in eredità da Tolomeo di 23؛ 51'
e che a lui fu dato di scoprire il moto dell'apogeo solare.
Queste variabilità indussero purtroppo gli astronomi arabi
ad ipotizzare la variabilità anche di un altro parametro
astronomico, quello del valore annuo della precessione. Ciٍ
fece nascere uno dei fantasmi dell'astronomia che imperversٍ
poi per più di mezzo millennio, cioè la trepidazione
Le speculazioni degli Arabi si potevano riassumere
grossolanamente cosى: tra l'epoca di Ipparco e quella di
Tolomeo (circa 270 anni) la variazione della precessione
appariva essere stata di circa 1؛ ogni 100 anni, mentre tra
le osservazioni di Tolomeo e quelle arabe dei secoli IX e X,
il rateo dava il valore di 1؛ ogni 66 anni. Contrariamente
all'opinione del grande Al Battani che aveva saggiamente
concluso che soltanto le accurate osservazioni dei secoli a
venire avrebbero potuto stabilire se il rateo doveva essere
considerato variabile o costante, nel secolo IX nacque la
teoria della variabilità di entrambi i parametri,
dell'obliquità e della precessione secondo un unico
meccanismo. Per tradizione la teoria è attribuita a
Thabit ibn Qurra (ca. 824 - 901), di cui abbiamo già
dato alcune notizie.
Occorre ricordare che la teoria affondava nel passato.
Teone di Alessandria, il commentatore di Tolomeo del
secolo IV, nella sua introduzione alle Tabelle ridotte
di Tolomeo, parla di una strana dottrina che veniva
professata da antichi astrologi. Essi sostenevano che le
stelle si muovevano, verso est per 8؛ al rateo di 1؛ ogni 80
anni. Dopo di che il moto si stabiliva verso ovest, sempre
per 8؛ e sempre al rateo di 1؛ ogni 80 anni. Questo moto
alternato continuava da tempo immemorabile. Inoltre, quegli
astrologi fissavano all'anno 158 a.C. l'epoca nella quale il
moto aveva cambiato direzione, stabilendosi verso est.
Occorre dire che né Tolomeo né alcun altro autore greco,
tranne Teone di Alessandria, fece mai menzione di questa
antica diceria. E' stata avanzata l'ipotesi che questa
dottrina sia stata una erronea interpretazione del fatto che
i Babilonesi ponevano, anticamente, l'inizio dei segni
zodiacali equinoziali e solstiziali all'8؛ grado del
rispettivo segno. Occorre anche dire che un semplice calcolo
avrebbe dovuto mostrare, agli astronomi arabi del secolo IX
che c'era qualcosa che non andava in quelle antiche teorie.
Infatti, per eseguire uno spostamento di 8؛ al rateo di 1؛
ogni 80 anni, ci sarebbero voluti 640 anni e, se nel 158
a.C. era iniziato il movimento verso est, nell'anno 483
avrebbe dovuto aver luogo l'inversione, per cui al tempo di
Thabit le stelle avrebbero dovuto essere in moto verso
ovest, il che non era assolutamente vero: le osservazioni
arabe mostravano inequivocabilmente che, almeno dal tempo di
Ipparco, le stelle si erano sicuramente spostate di circa
14؛ verso est, senza alcuna inversione. |
|
LA TREPIDAZIONE SECONDO THABIT
Nella cosmologia medioevale la sfera delle stelle fisse
ricevette la denominazione di ottava sfera, perchè a
Sole, Luna e ai cinque pianeti erano assegnate sette sfere.
Il titolo latino dell'opera di Thabit che descriveva la
trepidazione era Dei moti dell'ottava sfera. |
|
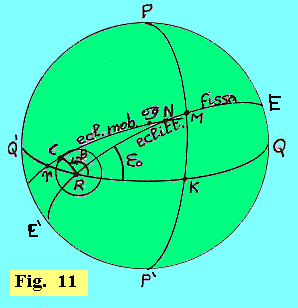
Thabit si proponeva di fornire una
spiegazione di due "fenomeni": la reale diminuzione
dell'obliquità dell'eclittica, e la supposta
variazione del rateo della precessione. All'uopo Thabit
circondava l'ottava sfera con una ulteriore sfera, che nella
cosmologia latina ricevette il nome di Primo mobile.
Questa nona sfera era quella che comunicava alla sfera delle
stelle fisse (e ai sistemi di sfere planetari interni di
origine tolemaica) il moto diurno, e quindi era quella che
portava l'equatore Q'RKQ. Questo equatore, fisso su
questa sfera, era intersecato in un certo suo punto R
dall'eclittica fissa E'RNME. Questa non era
l'eclittica reale ma una fittizia, facente un angolo
fisso di 23؛ 33' (secondo Thabit) con l'equatore del
Primo mobile. PMKP' è il coluro solstiziale fisso.
Nel punto R Thabit pone un cerchio, pure fisso,
avente raggio angolare ampio 4؛ 18' 43". Un altro
cerchio, simile al precedente, si trova centrato nel punto
di equatore diametralmente opposto ad R. Lungo il
cerchio centrato in R si muove di moto uniforme, nel
senso indicato dalla freccia, il punto C, che gli
astronomi latini chiamavano Caput Arietis. |
 |
|
(Questo punto C, pur muovendosi sul
cerchio fisso di centro R, appartenente al Primo mobile,
doveva intendersi (sempre secondo Thabit) appartenente
all'ottava sfera).
Il moto uniforme di C era tale che l'angolo
b variava di 360؛ in 4182 anni
islamici (circa 4057 anni giuliani). Diametricalmente
opposto a C c'è un punto, evidentemente anch'esso
mobile con lo stesso ritmo di C, e detto dagli
astronomi latini Caput Librae. Attraverso questi due
punti passava l ' eclittica mobile CN (anch'essa
appartenente all'ottava sfera). L'effettivo punto
equinoziale primaverile ^
risultava dall'intersezione di questa eclittica mobile con
l'equatore fisso.
L'eclittica mobile apparteneva dunque all'ottava sfera
(assieme alle stelle fisse che sono appunto fisse su di
essa), per cui il moto del punto C faceva muovere
l'eclittica mobile e tutte le stelle della stessa
quantità, onde la distanza angolare tra C e una certa
stella che fosse capitata su questa eclittica mobile,
sarebbe rimasta costante. Il punto N, di intersezione
dell'eclittica mobile con la fissa, era sempre a 90؛ da C,
ed era detto Caput Cancri. Esso aveva quindi un moto
di avanti e indietro sull'eclittica fissa, e non era
l'effettivo punto solstiziale, quello in cui il Sole vero
raggiunge la massima declinazione (questo punto è indicato
in figura con a.
Rispetto alla distanza dall'eclittica mobile quindi, la
latitudine celeste rimane costante. La longitudine invece
varia perchè la distanza angolare delle stelle dal punto
^ è continuamente variabile
(come vedremo tra poco). Il moto di avanti e indietro delle
stelle dell'ottava sfera implica una variazione di posizione
delle stelle rispetto all'equatore della nona sfera, e
quindi ascensione retta e declinazione saranno continuamente
variabili. |
|
ACCESSO E RECESSO DI THABIT
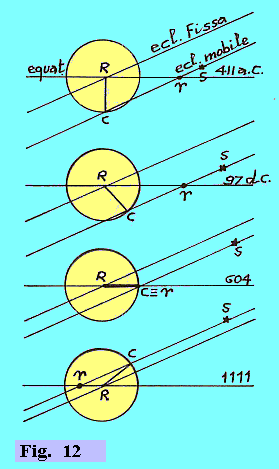
Volendo addentrarci (ancora per poco) nell'argomento
trascendente della trepidazione, osserviamo la figura 12,
che dà quattro situazioni del raggio RC, ad
intervalli di 507 anni, durante i quali il detto raggio
ruota di angoli b eguali di 45؛.
Come si vede, la distanza angolare della stella S dal
Caput Arietis C rimane costante (è stata scelta una
stella S giacente sull'eclittica mobile, per cui la
sua latitudine rimane sempre zero). La longitudine di S,
invece, essendo la distanza angolare di S da
^, varia in maniera
irregolare. Si vede infatti che la longitudine aumenta di
una quantità maggiore dall'anno 97 all'anno 604, di quanto
non sia aumentata dall'anno 411 a.C. all'anno 97.
In ogni caso, la longitudine ^S
è data da : ^S = CS +
^C, con CS costante
come detto, e ^C
positivo quando C è sopra l'equatore, e negativo
quando è sotto. ^C
(che, per un dato istante, ha lo stesso valore per tutte le
stelle), nella teoria della trepidazione è detta
equazione in longitudine. |
 |
|
Thabit non affrontٍ il problema di dare una
formula trigonometrica per l'equazione in longitudine
^C. Diede una tabella di
valori di ^C in funzione
dell'angolo b, da 0؛ a 90؛. I
valori di questa tabella si accordano abbastanza bene con la
formula sen(^C) = sen(10؛
45')•sen(b), che venne
largamente usata in seguito.
Dal De motu stellarum risulta chiaramente che Thabit
era consapevole che questo moto alternativo produceva anche
una variazione nell'obliquità, ma non si soffermٍ a trattare
con calcoli questo aspetto, si limitٍ a dare alcuni valori.
E' stato comunque calcolato recentemente che il modello di
Thabit comportava una variazione dell'obliquità tra 23؛59' e
23؛29', che corrispondono proprio ai valori entro i quali
l'obliquità era variata dall'antichità ai tempi di Thabit.
Eseguendo altri calcoli con formule più precise, si è
determinato che il sistema di Thabit dava risultati in linea
con ciٍ che si sapeva della precessione dai tempi di
Ipparco. Infatti, secondo queste formule precise dall'epoca
di Ipparco all'epoca di Tolomeo si avrebbe un rateo di 1؛ in
101 anni, mentre dall'epoca di Tolomeo fino all'epoca di
Thabit il rateo sarebbe di 1؛ in 64؛ anni (ricordiamo che
Thabit riteneva valido per il suo periodo il rateo di 1؛ in
66 anni). |
|
LA TREPIDAZIONE NEI SECOLI SUCCESSIVI
Nel mondo islamico orientale questa teoria della
trepidazione non venne accolta propriamente con favore.
Al-Battani adottٍ un rateo uniforme di 1؛ in 66 anni (Thabit
sostenne che in seguito anche al-Battani accettٍ la teoria).
Ibn Yunus (1100) adottٍ un rateo costante di 1؛ in 70 anni,
molto preciso per la sua epoca.
In Occidente ebbe un'accoglienza migliore. Le tabelle di
Thabit vennero incluse nelle Tavole toledane e ciٍ
contribuى enormemente alla popolarità della teoria stessa. A
partire dal secolo XIII l'aumento costante della precessione
avrebbe dovuto porre fine a qualunque idea di variabilità.
Invece, nelle Tavole Alfonsine venne introdotta una
teoria per la quale le stelle subivano una precessione
costante che faceva loro compiere un giro completo di sfera
celeste in 49000 anni, e a questo movimento costante veniva
sovrapposta una oscillazione di ± 9؛ che si completava in un
periodo di 7000 anni. Questa teoria, consacrata dalle
Tavole Alfonsine divenne standard in Europa dal XIV al
XVI secolo. |
|
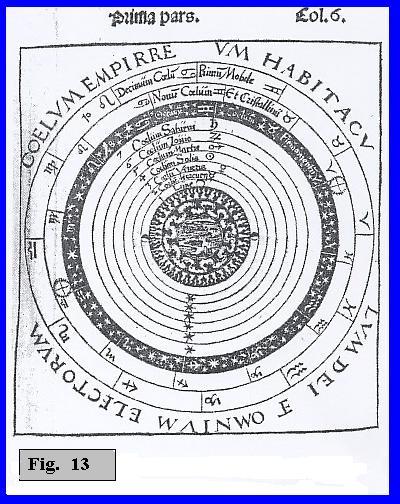
Era inevitabile che lo sdoppiamento della
precessione venisse "spiegato" con l'introduzione di una
ulteriore sfera (omaggio a Pitagora). L'illustrazione della
Fig. 13 è tratta da un famoso libro, il Cosmographicus
liber, scritto ed edito nel 1524 da Petrus Apianus
(Peter Bienewitz, 1495 - 1552). La figura mostra al centro
la Terra, circondata dalle sette sfere planetarie, a partire
dalla Luna. L'ottava sfera, quella delle stelle fisse
(nera), è chiamata Firmamento. La nona sfera, che
Apiano chiama Cristallino, porta i due cerchi sui
quali si muovono il Caput Arietis e il Caput Librae. Il
cerchio del Caput Arietis è situato, correttamente, proprio
prima dell'inizio della costellazione di Ariete. Notare come
ci sia una piccola differenza tra l'inizio del segno di
Ariete della nona sfera e l'inizio della costellazione di
Ariete dell'ottava: questa differenza è attribuita alla
componente variabile della trepidazione. |
 |
|
Invece la notevole differenza che c'è tra
l'inizio dei due segni, della nona e della decima sfera
(quest'ultima detta Primo mobile) indica l'effetto
sulla precessione della componente fissa. Infine, anche
Apiano, come Dante, circonda il cosmo con la sfera dell'Empireo,
residenza di Dio e di tutti gli eletti. Anche in una
edizione del Theoricae novae planetarum del famoso
Georg Peurbach pubblicato a Parigi nel 1553, viene data
la teoria originale della trepidazione di Thabit. Bisognerà
attendere un astronomo dell'autorità di Tycho Brahe
per togliere definitivamente la trepidazione dall'astronomia
europea, alla fine del secolo XVI. |
Pagina iniziale |
Il Ritorno all'Islam |
Libri Islamici |
Articoli |